Zahlen und deren Symbole in früheren Kulturen
Veröffentlicht - 15.März.2025
Das Zählen und die Zahlen sind wohl die grundlegendsten Ideen der Mathematik, auch historisch lässt sich das bestätigen, die erste mathematische Operation der Menschheit war das Zählen. Artefakte, welche bis zur Steinzeit zurückgehen, beweisen dies. Aber was bedeutet eigentlich Zählen bzw. was verstehen wir unter Zahlen? Um später zu verstehen, welche mathematischen Leistungen schon vor tausenden von Jahren erbracht wurden, widmen wir uns der vorangegangenen Frage.
Über das Zählen und die Zahlen
Denken wir ans Zählen ist jedem klar „wie das geht“ hinter diesem uns so offensichtlich erscheinenden Vorgang stecken aber einige Prinzipien.
- Eindeutigkeitsprinzip – Jedem „zu Zählenden“ wird genau ein Zahlwort zugeordnet (d. h. 1,2,3,4 usw. kommen nur einmal vor).
- Prinzip der stabilen Ordnung – Die Zahlwörter haben eine fixe Reihenfolge, in der keins ausgelassen werden darf.
- Kardinalzahlprinzip – Die letzte Zahl, welche zum Abzählen der „zu zählenden Dinge“ genutzt wird, entspricht der Anzahl der Dinge.
- Abstraktionsprinzip – Die „zu zählenden Dinge“ brauchen keine gemeinsamen Merkmale.
- Prinzip der beliebigen Reihenfolge – Es ist egal, wie herum ich die Dinge zähle, das Zahlwort ist keine Eigenschaft des Objekts.
Ähnliches gilt für den Begriff der Zahl selbst, dieser lässt sich aus verschiedenen Perspektiven betrachten.
- Kardinalzahl - Eine Zahl gibt die Anzahl von Dingen an.
- Ordinalzahl
- Zählzahl - „Eins, zwei, drei, vier, fünf Semester studiere ich schon.“
- Ordnungszahl - „Mein fünftes Semester.“
- Maßzahl - Eine Zahl gibt das Maß einer Größe an.
- Operator - Eine Zahl gibt die Häufigkeit eines Vorgangs an.
- Rechenzahl - Eine Zahl kann mit mathematischen Operationen manipuliert werden.
Mit diesem Hintergrundwissen können wir uns mit den Zahlzeichen vergangener Kulturen beschäftigen.
Zahlzeichen in frühen Kulturen
Mathematische Schriften gehen zurück bis ins alte Ägypten, zu den wichtigsten Quellen zählen die Papyri Moskau (ca. 1850 v. Chr.) und die Papyri Rhind (ca. 1650 v. Chr.). Verglichen mit der altägyptischen Mathematik gibt es wesentlich mehr Quellen der Mathematik aus Mesopotamien. Der Grund ist recht einfach: Tontafeln halten länger als Papyri. Diese frühen Kulturen benutzten verschiedene Zahlzeichen, welche wir im Weiteren genauer untersuchen möchten.
Zahlensymbole in Ägypten
Die Hieroglyphen zählen wohl zu den prominentesten Zahlsymbolen. Das System war dezimal, und die Zahlen wurden durch das Aneinanderreihen der Symbole gebildet und die Werte der einzelnen Zeichen addiert. Für die Potenz von 10, bis zu 1000000 gab es besondere Symbole. Alle sieben Zehnerpotenzsymbole sind in der Tabelle 1 dargestellt.
| Hieroglyphen | 𓏺 | 𓎆 | 𓊢 | 𓆼 | 𓂭 | 𓆐 | 𓁨 |
| Zahl | 100 | 101 | 102 | 103 | 104 | 105 | 106 |
Aufgabe
Schreiben Sie die folgenden Zahlen in dem uns bekannten Zehnersystem.
- 𓏺 𓏺
- 𓏺 𓏺 𓏺 𓏺 𓏺 𓏺
- 𓎆 𓎆 𓎆 𓏺 𓏺 𓏺 𓏺 𓏺 𓏺
- 𓆼 𓆼 𓆼 𓆼 𓊢 𓎆 𓎆 𓎆
Lösung
- 𓏺 𓏺 = 2
- 𓏺 𓏺 𓏺 𓏺 𓏺 𓏺 = 5
- 𓎆 𓎆 𓎆 𓏺 𓏺 𓏺 𓏺 𓏺 𓏺 = 35
- 𓆼 𓆼 𓆼 𓆼 𓊢 𓎆 𓎆 𓎆 = 4130
Aufgabe
Schreiben Sie die folgenden Zahlen mithilfe der Hieroglyphen der
Ägypter.
- 3
- 7
- 68
- 78540
Lösung
- 3 = 𓏺 𓏺 𓏺
- 7 = 𓏺 𓏺 𓏺 𓏺 𓏺 𓏺 𓏺
- 68 = 𓎆 𓎆 𓎆 𓎆 𓎆 𓎆 𓎆 𓏺 𓏺 𓏺 𓏺 𓏺 𓏺 𓏺 𓏺
- 78540
Zum Multiplizieren zweier Zahlen nutzen die Ägypter das folgende Verfahren.1
| 23 | 37 |
| 11 | 74 |
| 05 | 148 |
| 02 | |
| 01 | 592 |
| 851 |
Man schreibt die zu multiplizierenden Zahlen nebeneinander.
Die Linke der beiden wird halbiert, und falls nicht ganzzahlig abgerundet. Das Ergebnis wird unterhalb der ursprünglichen Zahl notiert. Der Vorgang wird wiederholt, bis man zur Eins gelangt.
Die rechte Zahl wird verdoppelt und das Ergebnis, wie links, unterhalb der ursprünglichen Zahl notiert.
Die rechten Zahlen werden gestrichen, wenn die zugehörige Linke gerade ist.
Die Summe der rechten, nicht gestrichenen Zahlen ist das zu bestimmende Produkt.
Aufgabe
Berechnen Sie 333 ⋅ 127 mithilfe des
ägyptischen Verfahrens.
Lösung
Mithilfe des obigen Verfahrens gilt:
| 333 | 127 |
| 166 | |
| 83 | 508 |
| 41 | 1016 |
| 20 | |
| 10 | |
| 5 | 8128 |
| 2 | |
| 1 | 32512 |
| 42291 |
Die Ägypter kannten auch schon (positive) Brüche, besonders ist aber, dass in ihrer Notation Brüche als Summe von Stammbrüchen (Brüche mit dem Zähler 1) dargestellt wurden. Solche Zerlegungen von Brüchen in Stammbrüchen werden heute als ägyptische Brüche bezeichnet. Die Darstellung eines Stammbruchs $\frac{1}{n}$ bestand aus zwei Hieroglyphen:
der Mund 𓂋 stand für den Zähler und den Bruchstrich,
das Zahlsymbol stand für den entsprechenden Nenner
So entspricht $\substack{𓂋 \\ 𓆼}$ dem Stammbruch $\frac{1}{1000}$. Wie kann ich nun aber z. B. zu dem Bruch $\frac{43}{59}$ eine Darstellung ägyptischer Form finden? Hierzu bietet sich folgender Algorithmus an:
Algorithmus
Gegeben sei ein Bruch der Form $\frac{a}{b}$ mit a, b ∈ ℕ.
Führe die Division $\frac{b}{a}$ durch, um einen Dezimalwert zu erhalten.
Bestimme die kleinste ganze Zahl n, die größer oder gleich dem Dezimalwert ist, der aus der Division resultiert. Das bedeutet, dass $n= \lceil \frac{b}{a} \rceil$ (die kleinste ganze Zahl, die den Wert der Division übersteigt). Der größte enthaltende Stammbruch ist dann $\frac{1}{n}$.
Subtrahiere den größten Stammbruch $\frac{1}{n}$ von $\frac{a}{b}$. Das ergibt den Rest $$\frac{a}{b} - \frac{1}{n} = \frac{a \cdot n - b}{b \cdot n}.$$
Wenn $\frac{a \cdot n - b}{b \cdot n}$ ein Bruch mit dem Zähler 1 ist (d.h. der Bruch ist ein Stammbruch), stoppe die Berechnung. Andernfalls gehe zurück zu Schritt 1 mit dem neuen Bruch $\frac{a \cdot n - b}{b \cdot n}$.
Gib alle gefundenen Stammbrüche in Summe aus.
Für $\frac{43}{59}$ gilt dann $$\frac{43}{59}=\frac{1}{2}+\frac{1}{5}+\frac{1}{35}+\frac{1}{4130}.$$ Dass der obige Algorithmus immer funktioniert, bleibt hierbei offen, es lässt sich aber durch Kontradiktion beweisen, was hier aus Zeitgründen ausgespart wird. Es ist wichtig anzumerken, dass die ägyptische Form eines Bruchs nicht eindeutig ist. Es lässt sich ebenfalls beweisen, dass jeder Bruch unendlich viele ägyptische Formen besitzt.
Aufgabe
Bestimmen Sie die ägyptische Form von $\frac{27}{55}$.
Lösung
Nach obigem Algorithmus gilt $\frac{55}{27}\approx 2.04$ also n = 3. Somit ist der größte Stammbruch $\frac{1}{3}$. $\frac{27}{55}-\frac{1}{3}= \frac{81}{165}- \frac{55}{165}= \frac{26}{165}$, das ist kein Stammbruch, also wieder von vorne. $\frac{165}{26} \approx 6.35$ also n = 7. Somit ist der nächstgrößte Stammbruch $\frac{1}{7}$. $\frac{26}{165}-\frac{1}{7}= \frac{182}{1155}- \frac{165}{1155}= \frac{17}{1155}$, das ist kein Stammbruch, also wieder von vorne. $\frac{1155}{17} \approx 67,9$ also n = 68. Somit ist der nächstgrößte Stammbruch $\frac{1}{68}$. $\frac{165}{1155}-\frac{1}{68}= \frac{1156}{78540}- \frac{1155}{78540}= \frac{1}{78540}$, das ist ein Stammbruch, also sind wir fertig. $$\frac{27}{55}=\frac{1}{3}+\frac{1}{7}+\frac{1}{68}+\frac{1}{78540}$$
Zahlensymbole der Mesopotamier
Die Mesopotamier benutzen die in Abbildung 1 festgehaltenen Symbole.2
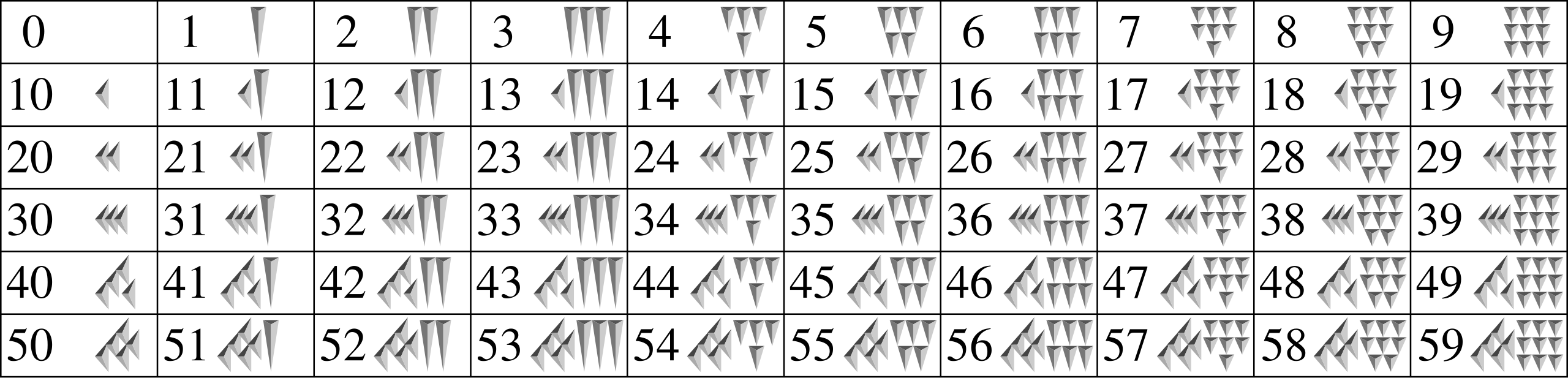
In diesem System stellen Ziffern weiter links größere Werte dar, ähnlich wie im modernen Dezimalsystem, wobei die Basis 60 statt 10 war.
Das Zahlensystem der Mesopotamier ist das älteste Positionssystem. Jedoch hat es seine Tücken, es fehlte ein Zeichen für fehlende Potenzen von 60 also, für die Ziffer 0. So haben 10 ⋅ 60 + 1, 10 ⋅ 603 + 1 ⋅ 601 oder 10 ⋅ 602 + 1 ⋅ 60−1 dieselbe Keilsequenz. Der exakte Zahlwert lässt sich somit nur aus dem Kontext ermitteln. Ein Zeichen für die Null wurde erst in der Zeit der Perser eingeführt. Sie diente aber nur „inneres Lückenzeichen“.
Andere Zahlensymbole vergangener Kluturen
Maya
Die Maya entwickelten eine Zahlschrift, welche aus Punkten und Strichen bestand. Damit stellten additiv die Zahlen von 1 bis 19 dar. Zahlen größer als 19 wurden mithilfe eines Stellenwertsystems dargestellt. Anders als bei dem uns heute bekannten Zehnersystems ordneten die Maya ihre Zahlen der Größe nach von unten nach oben.
Römer
Einige der Zahlensymbole der Römer sind in der Tabelle 2 dargestellt.
| Zeichen | I | V | X | L | C | D | M |
|---|---|---|---|---|---|---|---|
| Zahl | 1 | 5 | 10 | 50 | 100 | 500 | 1000 |
Besonders an diesen Zahlensymbolen ist die abwechselnde Fünfer-Zweier-Bündelung. Das birgt spätestens beim Addieren zweier römischer Zahlen große Schwierigkeiten, weil sich hier nicht ohne Weiteres schriftlich addieren lässt.
Literatur
- Brückler, F. M. (2017). Geschichte der Mathematik kompakt. In Springer eBooks. https://doi.org/10.1007/978-3-662-55352-7
- Padberg, F. & Benz, C. (2020). Didaktik der Arithmetik: fundiert, vielseitig, praxisnah. Springer Spektrum.
- Schipper, W. (2009). Handbuch für den Mathematikunterricht an Grundschulen.